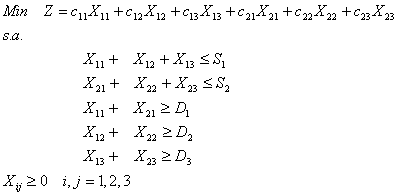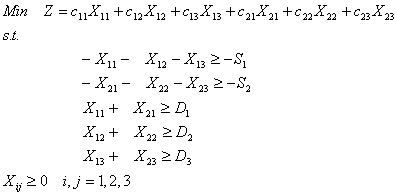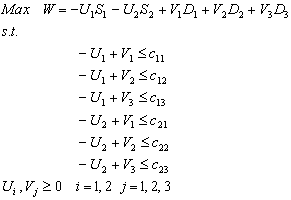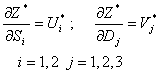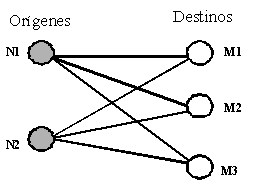
Referencia

Introducción

El término “Problema del Transporte” está ligado a la literatura de Investigación de Operaciones como una aplicación exitosa para resolver el problema de distribuir carga de la manera más económica desde los orígenes donde ésta se encuentra hasta los destinos donde es requerida, dados los costos de transporte desde cada origen hasta cada destino.

Aunque este problema es uno de los modelos comúnmente discutidos en las aplicaciones de la Investigación de Operaciones, probablemente el trabajo más antiguo conocido de este modelo se debe a G. Monge, matemático francés del siglo XVIII (Schrjiver, 1986). De acuerdo a Appell (1928), Monge publicó en 1781 Le Problème Géométrique des Déblais et Remblais (El Problema Geométrico del Movimiento y Relleno de Tierras) en las memorias de la Academia Francesa de Ciencias. Aunque Monge estaba interesado básicamente en geometría, propone el problema de minimizar el costo total de mover tierra desde varios orígenes para rellenar en varios destinos como sigue:

“Dados dos volúmenes equivalentes, descomponerlos en partículas infinitamente pequeñas, correspondiéndose uno-a-uno, de modo tal que la suma de los productos de los recorridos hechos para llevar cada partícula sobre su contraparte, por el volumen de la parte movida, sea un mínimo”.(citado en Appell 1928, p.1).[1]

Como lo describe Taton (1951), el interés de Monge en problemas de movimiento de tierras tuvo que ver con su disposición a resolver problemas de ingeniería militar relativos a la construcción de fuertes. Su percepción de los costos implicados en la tarea, es una cruda aproximación al costeo por tonelada-kilómetro que se usa en nuestros días:

“El precio del transporte de una molécula dada, manteniendo todo lo demás igual, es proporcional a su peso y a la distancia que recorre, de modo que el precio total del transporte es la suma de los productos de la moléculas multiplicadas cada una por la distancia recorrida  .” (citado por Taton 1951, p. 194).[2]

El Problema del Transporte

Si bien Monge usa un lenguaje geométrico discutiendo puntos, líneas y partículas infinitamente pequeñas, el problema que plantea corresponde al Problema del Transporte, en el cual hay N orígenes con cantidades conocidas de un cierto producto disponible, M destinos con demandas conocidas del producto y todos los costos de transporte para cada par origen-destino son conocidos.

La Figura 1 ilustra el problema con dos orígenes y tres destinos, con el objetivo de encontrar el plan de costo mínimo para distribuir los productos en los orígenes y satisfacer las demandas en los destinos.

Figura 1

 Un ejemplo del problema del transporte

El problema del transporte resurgió en la década de 1940 dentro de la corriente de trabajos planteados con el nacimiento de la Investigación de Operaciones como una disciplina autónoma. El problema fue considerado en 1941 por Hitchcock e independientemente por Kantorovich en 1942 y por Koopmans en 1947. El modelo de Hitchcock plantea encontrar el mínimo costo de distribuir un producto desde varias fábricas a un número dado de ciudades, y desde entonces el modelo es conocido también como el Problema de Transporte de Hitchcock. En 1951, G. Dantzig desarrolló la primera solución al problema, utilizando programación lineal (Arnoff & Segupta, 1961).

A pesar de su simplicidad, el problema del transporte contiene ya algunos de los elementos básicos que se han utilizado en subsiguientes esfuerzos de modelación del transporte de carga:

a)     Una función objetivo, esto es, el costo total del plan de transporte, que refleja el objetivo del decisor, así como un criterio mensurable para la transportación involucrada, es decir, la tonelada-kilómetro (considerando la distancia como costo).

b)     Las restricciones del problema, esto es, las distintas ofertas de productos en los orígenes y las respectivas demandas en los destinos, y

c)      Los parámetros del problema, es decir, los costos para los distintos enlaces origen-destino que representan las características de la red carretera.

Cabe notar, sin embargo, que el problema del transporte no puede hacer explícita la topología de la red carretera, ni puede considerar diferencias en los costos percibidos por los transportistas ni diferencias en las capacidades de los vehículos que mueven las cargas. Esto ha dado lugar a otros desarrollos en la modelación del transporte de carga, que buscan hacer modelos más realistas cada vez, como es el caso del modelo gravitacional para distribución de viajes (Ortúzar & Willumsen, 1994, pp. 394-395).

La formulación con Programación Lineal

El problema del transporte puede verse como la simplificación del objetivo de minimizar los costos del transportista que mueve carga desde los orígenes a los destinos para satisfacer la demanda. El planteamiento del problema de transporte como un programa lineal, junto con la interpretación dual de éste permite visualizar un segundo punto de vista del problema, donde el interesado es el embarcador que intenta satisfacer la demanda en los destinos, tratando de maximizar el beneficio que le representa la operación.

El planteamiento es como sigue: llamando X_ij al flujo de productos del origen  i  al destino  j  , c_ij al costo unitario por tonelada movida, S_i a la oferta de producto en el nodo i  , D_j  a la demanda de productos en el nodo j, y Z al costo total del plan de transporte, entonces para el caso con dos orígenes y tres destinos, el programa lineal es:

…[1]

Éste es el problema del transportista que busca satisfacer la demanda en los destinos a un costo total mínimo. Las restricciones del programa representan la conservación del flujo en los nodos, impidiendo al transportista planear movimientos de carga mayores a la disponibilidad en los orígenes y obligándolo a entregar en los destinos al menos la demanda solicitada. Para fines de presentación, el problema es puesto en la forma canónica de un programa lineal para minimización (con restricciones ³):

…[2]

Así, escribiendo el dual del problema anterior resulta:

…[3]

Una interpretación económica del problema dual aclara el “segundo punto de vista” implícito en el problema del transporte original, que corresponde al interés del embarcador.  Llamando U₁ y U₂ a los precios del producto a los que el embarcador compra en los orígenes 1 y 2, y V₁, V₂, V₃ al precio del producto que los consumidores pagan en los destinos 1, 2 y 3 respectivamente, resulta que el objetivo del programa dual es el del embarcador que compra el producto en los orígenes y lo vende en los destinos, tratando de maximizar la utilidad de la operación expresada en la función objetivo dual: (ingreso) - (costo de compra). Las variables duales U_i y V_j son llamadas usualmente “precios sombra”.

Conforme a la interpretación económica para el problema dual propuesta por Bazaraa et al (Bazaraa et al, 1990, p.254-256), si Z^* e la solución óptima del programa primal [2] y la demanda es ligeramente alterada en los nodos, de modo que la solución óptima no cambie, entonces las variables duales (precios sombra) satisfacen:

                   …[4]

Estas ecuaciones [4] muestran que los precios sombra U_i^* and V_j^* cambian con la tasa de cambio del costo óptimo de transporte Z^* con respecto a la oferta en los orígenes o a la demanda en los destinos. Así, por ejemplo, al aumentar una unidad la demanda D₁ en el destino 1, aumenta el costo óptimo Z^* por V₁^*, y éste sería el precio justo (precio sombra) que los consumidores en el destino 1 tendrían que pagar para obtener ésa demanda adicional.

Respecto de las restricciones, para un par de origen  i  y destino  j, la restricción dual:

que se reescribe como:

  …[5]

indica que el precio V_j en el destino  j  no puede exceder la suma del precio en el origen  i  (U_i ) más el costo del transporte involucrado c_ij. A esta condición se refiere Harker (1987) como el Equilibrio de Cournot en su discusión sobre los modelos de equilibrio espacial de precios.

En las propias palabras de Cournot:

   “Es evidente que un artículo capaz de ser transportado debe fluir del mercado donde su valor es menor al mercado donde su valor es más grande, hasta que la diferencia en valor, de un mercado al otro, no represente más que el costo del transporte.” (Cournot, 1838, p. 117).[3]

Adicionalmente, resulta de interés que la teoría de dualidad garantiza que en la solución óptima, tanto el objetivo del problema primal como el del dual tienen el mismo valor, con lo que tanto el transportista como el embarcador pueden lograr simultáneamente sus óptimos.

Conclusiones

Dentro del enfoque de planeación del transporte usado en la actualidad, el planteamiento del problema del transporte (representado al transportista) y su problema dual asociado (representando al embarcador) permite apreciar una condición comúnmente encontrada en el modelado del transporte de carga: la existencia de múltiples actores que intervienen en la generación de los flujos de carga, y que usualmente tienen objetivos distintos, y en ocasiones hasta opuestos. En el caso del problema del transporte, la solución óptima afortunadamente satisface tanto al transportista como al embarcador, pero ésta es una situación que generalmente no ocurre en el transporte de carga. Cuando los distintos actores en el transporte de carga tienen objetivos que se oponen, la tarea de modelado exige buscar enfoques adecuados para representar la solución de conflictos.

Así pues, la modelación del transporte de carga conlleva la dificultad de buscar técnicas matemáticas para representar adecuadamente a los múltiples actores que determinan los flujos de carga, y sus distintos objetivos, cuando todos estos actores tratan de optimizar sus propios criterios de desempeño simultáneamente aún cuando estos objetivos se contrapongan. Entre los enfoques reportados en la literatura, técnicas como la Teoría de Juegos, la programación por objetivos o la programación bi-nivel han mostrado ser perspectivas promisorias para la modelación del comportamiento del transporte de carga (Moreno, 2004), aportando de este modo nuevas herramientas analíticas para el planificador del transporte.

Bibliografía

Appell, P. “Le probléme géométrique des déblais et ramblais”. (in French). Gauthier-Villars. Paris. [online]. Available at:URL:http://gallica.bnf.fr. [Accessed January 2003]. 1928.

Arnoff, E.L. and Sengupta, S.S. Mathematical programming. In: “Progress in Operations Research”. Vol. I. Edited by Russell L. Ackoff. John Wiley & Sons. USA. 1961.

Bazaraa, M.S., Jarvis, J.J. and Sherali, H.D. “Linear programming and network flows”. John Wiley & Sons. Singapore. 1990.

Cournot, A. “Researches into the mathematical principles of the theory of wealth”. Translated by Nathaniel T. Bacon. The Macmillan Co. New York, 1927. 1838.

Harker, P.T. Issues and models for planning and regulating freight transport systems. In: “Lecture Notes in Economics and Mathematical Systems”. Lucio Bianco and Agostino La Bella, editors. International Seminar on Freight Transport Planning and Logistics, Italy. Springer-Verlag.pp. 374-408. 1987.

Moreno, E. Planner-user interactions in road freight transport. “A modelling approach with a case study from Mexico”. (PhD Thesis). Institute for Transport Studies, University of Leeds. United Kingdom. 2004.

Ortúzar, J.D. and Willumsen, L.G. “Modelling Transport”. 2nd edition. Chichester, UK. John Wiley & Sons. 1994.

Schrijver, A. “Theory of Linear and Integer Programming”. John Wiley & Sons. Chichester. pp 376-377. 1986.

Taton, R. “L’oeuvre scientifique de Monge”.  Presses Universitaires de France. Paris. pp. 193-196. 1951.

Eric MORENO Q.