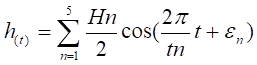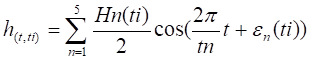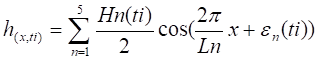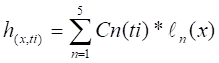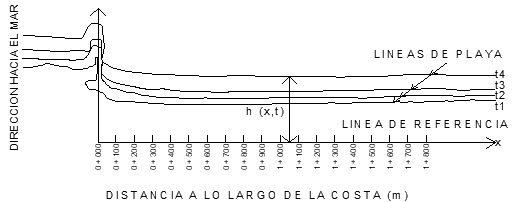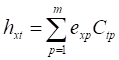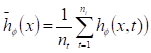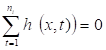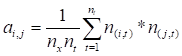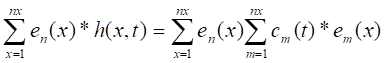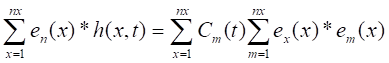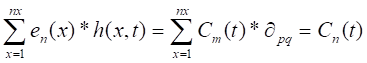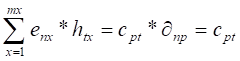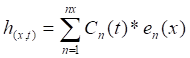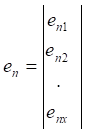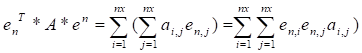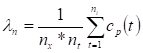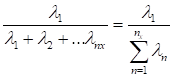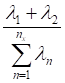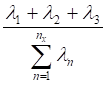Resumen

Es de vital importancia resaltar las modelaciones numéricas que se realizan de la evolución de la línea de playa, así como del movimiento de arena en el fondo del mar sobre todo en la zona de rompientes. Al realizar dichas modelaciones numéricas para analizar la evolución del fondo del mar, se debe conocer la distribución de las corrientes debidas al oleaje y a las mareas, posteriormente se determinará la cantidad de arena suspendida y removida por efecto del oleaje, así como la cantidad que es transportada por las corrientes, lo cual requiere una metodología extensa para realizar diversas cuantificaciones de la evolución de la línea de playa.

Por lo anterior se utiliza un método de modelación numérica que se fundamenta en la teoría de una línea, y para el cual es necesario encontrar la tendencia de la evolución de la línea de playa, mediante el análisis de eigenfunciones empíricas a datos obtenidos de los cambios en la línea de playa.

En álgebra lineal, los vectores propios o eigenvectores de un operador lineal son los vectores no nulos que, cuando son transformados por el operador, dan lugar a un múltiplo escalar de sí mismos, con lo que no cambian su dirección. Este escalar λ recibe el nombre valor propio, valor característico o eigenvalor. A menudo, una transformación queda completamente determinada por sus vectores propios y valores propios. Un espacio propio o eigenespacio es el conjunto de vectores propios con un valor propio común.

 

 

Conceptualización del análisis de eigenfunciones empíricas.

 

Dado que el análisis con Eigenfunciones  empíricas es fundamentalmente similar al análisis de Fourier, los conceptos básicos de análisis mediante las Eigenfunciones empíricas se explicarán con base en la ecuación que gobierna la energía espectral del oleaje.

 

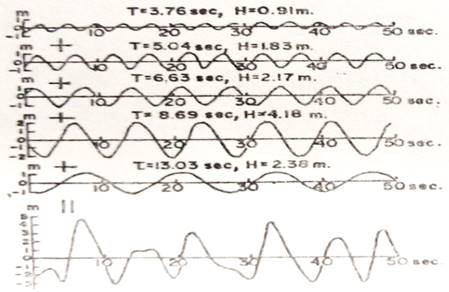
En la Fig. 1, se muestra el registro típico del oleaje que se presenta en el mar, descompuesto en 5 oleajes sinusoidales (componentes del oleaje). Pudiéndose expresar analíticamente el registro del oleaje real por la siguiente ecuación:

 

                               ec. 1

 

Dónde:

	Nivel de la superficie del oleaje en el tiempo t
	Número de componentes (en este caso 5)
	Altura del oleaje de la componente n
	Periodo del oleaje de la componente n
	Ángulo de fase de la componente n, con lo cual se toma en cuenta, el que el origen común de ese oleaje  no corresponda al origen común seleccionado para todas las componentes.

 

 

 

Fig. 1. Oleaje irregular y su descomposición en componentes.

 

 

El registro de oleaje de la Fig. 1, corresponde a un segmento de oleaje durante un periodo de tiempo t = t₁. Si tomáramos registros de oleaje de otros tiempos (t = t₂, t₃, ….), tendríamos diferentes formas de oleaje irregular. Sin embargo podríamos nuevamente obtener para los oleajes irregulares medidos, su descomposición en las cinco componentes como se realizó en la Fig. 1. 

 

En otras palabras, cada registro de oleaje irregular podrá expresarse por la composición de las cinco componentes básicas establecidas en la Fig. 1, con diferente altura y ángulo de fase (,) como:

 

t_{i =} t_1, t_2, t_3……….

 

     ec. 2

 

Consideremos lo anterior en otra condición física, por ejemplo, en perfiles playeros ó en configuraciones de la línea de costa.

 

Si la abcisa de la Fig. 1, se cambia de unidades de tiempo (t) a unidades de distancia a lo largo de la costa (x), la ec. 2, se puede expresar como:

 

                            ec. 3

 

Donde  Ln es la longitud de la componente topográfica n.

 

Una pregunta que resulta de importancia sería, si la ec. 3 es válida expresarla, cuando la línea de costa es irregular.

 

Para contestar lo anterior, regresemos brevemente al concepto del oleaje irregular. En el caso de oleaje irregular (oleaje real), este se puede descomponer en varias componentes sinusoidales como se indicó en la ec. 2, ya que existe un soporte teórico basado en la función sinusoidal (oleaje regular) de acuerdo a la teoría del oleaje de pequeña amplitud, y en el caso de la ec. 3 no se garantiza que la componente básica de la línea de costa corresponda a una función sinusoidal, resultado incorrecta  la ec. 3, al sobreponer las diferentes componentes de la línea de costa y expresando el resultado como n(x, t).

 

Para poder expresar las diversas componentes de la línea de costa por medio de funciones sinusoidales, Winant, Inman y Nordstrom en 1975, introdujeron el concepto de Eigenfunciones Empíricas en el campo de la ingeniería de costas. Este concepto se establece al considerar la función sinusoidal básica de la línea de costa como:

 

                                                                 ec. 4

 

Dónde:

(x)	Es la función básica de la línea de costa
(ti)	Es la amplitud correspondiente a    de la ec.  2.

 

La ec. 4 es válida con la limitación de que n(x) sea una función ortogonal.

 

El análisis de Eigenfunciones Empíricas corresponde al método de encontrar la relación de la ec. 4, donde la línea de costa se expresa como una combinación lineal de una función dependiente del tiempo (t)  y una función dependiente del espacio (x). En el caso del análisis de Fourier, la función sinusoidal está dada de manera anticipada por la función ortogonal, mientras que  en la ec. 4, la función ortogonal  (x)  es conocida anticipadamente.

En el análisis de Eigenfunciones empíricas, la función    se decidirá empíricamente basándose en los datos medidos en campo de la línea de costa, correspondiendo esto al origen del método de “Eigenfunciones Empíricas”.

 

 

Método analítico del análisis de eigenfunciones empíricas.

 

 

(1)         Expresión de datos de la línea de costa.

 

Si denotamos con   los datos de la línea de costa, donde x es la localización (x = 1, 2, 3,…, nx) sobre la línea de playa medida desde una línea de referencia y t es el tiempo cuando la línea de playa ya fue medida (t = 1, 2, 3,…, nt), ver Fig. 2.

 

Fig.  2  Convención de la línea de costa  en el método de Eigenfunciones Empíricas (Montoya R., J. M., 1988).

 

 

Los valores de (x = 1, 2, 3,…, nx) y (t = 1, 2, 3,…, nt), se pueden expresar como una combinación lineal de factores dependientes del tiempo  y factores dependientes de la localización de la línea de costa  como se indica en la ec. 5.

 

Conocida   como el valor relativo de la distancia  de algún punto de x sobre la línea de playa a partir de una línea base previamente definida, en algún tiempo, t, conforme a lo que se  muestra  en la figura anterior, entonces  se puede expresar como una combinación lineal de factores dependientes del tiempo  y factores dependientes del lugar  como se indica a continuación. (Montoya, J. M., 1988)

….………                                               

                             ec. 5

Donde;

; Es el valor relativo en algún  tiempo t, de la distancia de algún punto x  sobre la línea de playa a partir de la base.

; Función dependiente del espacio, llamado Eigenvector.

; Función dependiente del tiempo.

 

 

En 1975 cuando Winant introdujo el método de análisis de Eigenfunciones Empíricas en la ingeniería de costas, usó los datos de   directamente, sin embargo después de algunas consideraciones, es común que en este tipo de análisis se presenten desviaciones de los datos de la línea de costas respecto a la posición del tiempo medio (Katoh, Kazumasa, 1988). Esto significa, que se deberá de realizar la siguiente operación a los datos originales:

De acuerdo a Winant (1975),  el poder de esta técnica descansa en el hecho de que un conjunto de Eigenfunciones, tales como (ec. 5.3) no se selecciona sino más bien se genera el conjunto de funciones que mejor se ajuste a los datos, en el sentido de mínimos cuadrados.

 

Al aplicar el método de análisis de Eigenfunciones empíricas, se deberá aplicar la ecuación a los datos originales de la línea de playa.

……                                              ec. 6

Dónde:

	Es la distancia de la línea de playa en alguna localización x para algún tiempo t de los datos originales.
	Es el valor promedio de la línea de playa en cada punto, éste valor se calcula de acuerdo con la siguiente ec. 7.

 

                                                         ec. 7

Resultando válida la siguiente ecuación,

                                     ec. 8

 

 

(2)          Cálculo de la matriz simétrica de correlación

 

Usando los valores modificados de  , se puede calcular la matriz A de correlación simétrica formada por los siguientes elementos:

………ec. 9e              c. ec. 9

 

(3)         Eigenvalores de la matriz simétrica de correlación

 

La matriz simétrica  de correlación A,  posee un grupo de Eigenvalores   y un grupo correspondiente de Eigenvectores   definidos por la siguiente ecuación matricial:

………………………… 10 ec. 10

Generalmente es imposible, obtener analíticamente los Eigenvectores de la ec. 10, sin embargo, pueden calcularse por medio de métodos numéricos del algebra matricial usando computadora.

Así, la matriz A será una matriz simétrica real para los siguientes casos:

		0

                                                                                                ec. 11

Donde  es el delta de kronecker

El eigenvector   de la ec. 10 corresponde al  (x)  de la ec. 4. Como la función ortogonal   puede estimarse empíricamente por las ecs. 9 y 10 usando valores medidos de la línea de costa h(x, t), el eigenvector  , es llamado la Eigenfunción Empírica.

 

(4)         Determinación de la función dependiente del tiempo

 

Al multiplicar la ec. 4 por el eigenvector  n(x) se tiene la ec. 12:

 

                                                                                    ec. 12

 

 

Por consiguiente, el coeficiente C_m (t) se puede evaluar con el proceso desarrollado anteriormente. Pudiéndose concluir que el modelo de la ec. 4, puede ser estimado únicamente de los valores  h (x, t) medidos de la línea de costa.

 

 

 

Significado físico de eigenfunciones empíricas

 

 

 

Como resultado del análisis de Eigenfunciones empíricas se tiene la ecuación:

….…………..…………………………     ec. 13

 

 Donde la función de tiempo  corresponde a la amplitud del oleaje en el análisis espectral como se explicó en el inciso 2.1.

 

Así a continuación se estimará la magnitud de .

Del algebra matricial se sabe que:

   

Multiplicando la ec.10  por , se tiene:

                                                              ec. 14

Si el eigenvector n está definido como:

                                                ec. 15

 

 

El miembro de la izquierda de la ec. 14 se puede escribir como:

                           ec. 16

 

Cabe mencionar que la estructura del modelo puede estimarse únicamente a partir de los valores medidos .

 

El valor de la eigenfunción  se puede estimar a partir de la siguiente ecuación.

                                                                                              ec. 17

 

 

Así la magnitud de la  en los tiempos corresponden al valor de , se asume el siguiente orden:

 

					…
.		.		.	…		.
.		.		.	…		.
					…

 

Por lo tanto se puede resolver numéricamente para conocer  y , respectivamente.

Así el coeficiente  se puede evaluar con el proceso desarrollado anteriormente.  Con ello podemos concluir que el modelo de la ecuación de la energía espectral del oleaje puede ser estimada únicamente a partir de los valores de  medidos de la línea de costa.

 

En el caso de las Eigenfunciones empíricas, la aproximación también se conoce como modo, y comúnmente en el análisis de la evolución de la línea de playa, los resultados son satisfactorios cuando se calcula la Eigenfunción  y la función del tiempo hasta el tercer modo.

Así se tiene, que el análisis de la línea de playa  con eigenfunciones empíricas tienen las siguientes aproximaciones;

• Para la primera aproximación .
• Para la segunda aproximación 
• Para la tercera aproximación

Para la primera aproximación, la precisión se calcula con la siguiente ecuación:

Para la segunda aproximación, la precisión será:

 

Para la tercera aproximación, la precisión será: 

 

 

Aplicación del método de eigenfunciones empíricas

 

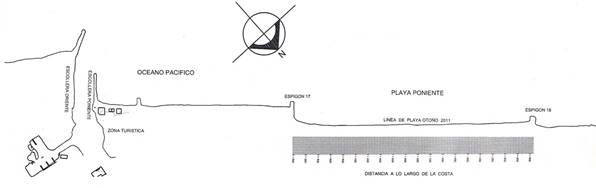
La aplicación del método de eigenfunciones empíricas se realizó a datos de la línea de playa, que comprenden la zona localizada entre el espigón 17 y el espigón18 ubicados en la playa poniente de Puerto Chiapas, Fig. 3. Las mediciones se recopilaron en una longitud de playa de 3,800 metros a partir del espigón 17.

 

 

Fig. 3  Línea de playa del levantamiento batimétrico

 

De la aplicación del método de eigenfunciones empíricas para el análisis de los cambios estacionales y anuales de la playa poniente de Puerto Chiapas, Chiapas, se  concluye que la dirección de oleaje predominante es la sur 45 grados oeste (S45°W), de acuerdo a los datos de la línea de playa retomados de lo levantamientos topobatimétricos, realizados en el periodo de enero a diciembre del 2001.

 

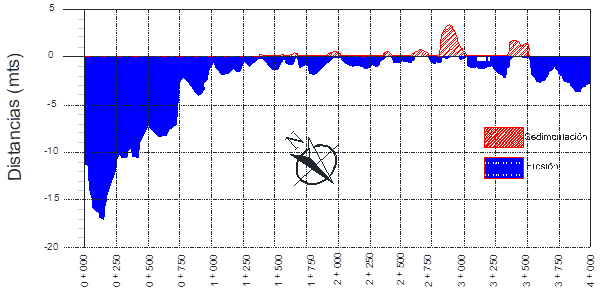
Del procesamiento de los datos a través de eigenfunciones obtuvimos que se tiene una precisión del  81.22% de manera estacional, con lo que se puede describir de manera mucha exactitud, los cambios estacionales y anuales para la línea de la playa poniente del puerto, con ello observamos que la playa presenta severas erosiones  a lo largo de la línea, Fig. 4.

 

Fig. 4  Análisis estacional de la costa.

 

 

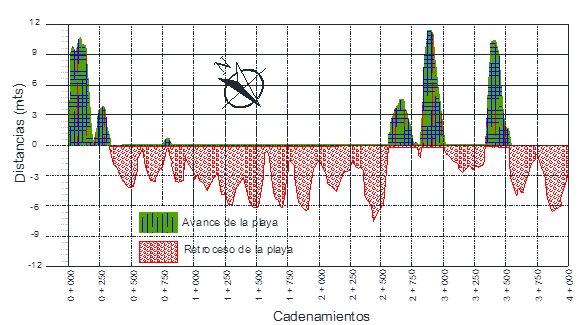
Fig. 5  Análisis  la evolución de la línea de playa

 

 

De manera anual la precisión obtenida del análisis con eigenfunciones empíricas, nos da una precisión del 11.98 %, Fig. 5,  por lo que con esta precisión fueron descritos  los cambios anuales de la línea de playa de puerto Chiapas.

 

Para efectos de este análisis se observa que el análisis  de los cambios estacionales y anuales de la línea de playa de puerto Chiapas, mediante la aplicación de eigenfunciones empíricas, si es representativo de lo que se genera en la realidad, y se demuestra al interpretar de manera precisa, los cambios estacionales y anuales de la línea de playa de la costa poniente de Puerto Chiapas que prevalecen en la actualidad.

 

Conclusiones

 

Con el análisis de datos de la línea de costa con Eigenfunciones Empíricas, la precisión está dada hasta la tercera aproximación como máximo.

El significado físico de los modos de las eigenfunciones empíricas, al analizar la evolución de la línea de costa es la siguiente:

Modo 1 de las eigenfunciones empíricas, indica los cambios anuales que sufre la línea de playa debido al transporte litoral.

Modo 2 de las eigenfunciones empíricas, indica los cambios estaciónales que sufre la línea de playa, debido al  transporte litoral, y en este caso se puede diagnosticar la dirección predominante del oleaje generador de éstos cambios.

 

Nomenclatura

 

 

 

Referencias bibliográficas consultadas

 

1.                                Montoya Rodríguez, J.M.

Descripción de los cambios estacionales y anuales de la línea de Playa del Puerto de Lázaro Cárdenas, Michoacán, usando Eigenfunciones  Empíricas, Ponencia Congreso Nacional de Ingeniería Marítimo Portuaria, Veracruz 1988.

2.                                Sato, Shoji, et all.

Análisis de datos de la línea de playa utilizando Eigenfunciones Empíricas.

3.                                Sato, Shoji, et all.

Experimento sobre la evolución de la línea de playa utilizando la teoría de una línea.

4.                                Juárez Rueda, Mercedes,

Experimento Numérico sobre Movimiento de Arena (Utilización de Eigenfunción Empírica y Teoría de un línea), Curso Internacional de Ingeniería Hidráulica Portuaria Puertos Mexicanos, 1999.

5.                                Davis, Richard,

Coastal Sedimentary Environments, second revised, capítulo Modeling Coastal environment, pp. 677-703.

6.                                Aubrey, D. G., Inman, D. L., y Winant, D. (1980)

The statical prediction of beach changes in southern California. J. Geophysical. Res. 86, 3264-3276

7.                                Resio, D. T., and B. P. Hayden (1973)

An integrated model of storm generated waves, Tech. Rep. 8,273 pp., Dep. of Environ. Sci., Univ. of Va. Charlottesville

8.                                Winant, C. D., Inman, D. L., y Nordstorm, C. E. (1986) 

Description of seasonal beach changes using Empirical Eigenfunctions. Journal of geophysics. Res., 80, 1957, 1979-1986

 

OCAÑA Karina
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.

ÁVILA Dora
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.

PORRES Adriana
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.

MENDOZA Manuel
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.

RAMÍREZ Rodolfo
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.